This tutorial explains the concepts of Dependency Inversion Principle which represents 'D' among the set of 5 S.O.L.I.D (an acronym) design principles. We will first look at the definition of Dependency Inversion Principle followed by an in-depth explanation of the Principle. We will then take a look at the advantage which is obtained when using the Dependency Inversion Principle. Next, the use of Adapter Pattern in enabling the use of the Principle in some cases is discussed. This is followed by a Java example demonstrating how classes and their dependencies in Java should be designed in line with the Dependency Inversion Principle. Dependency Inversion Principle Definition Depending on which source one refers to, Dependency Inversion Principle, as defined by Robert C. Martin, can be defined in any of the following ways
Depend upon Abstractions. Do not depend upon concretions.
OR
Abstractions should not depend upon details. Details should depend upon abstractions.
OR
High-level modules should not depend on low-level modules. Both should depend on abstractions.
Understanding the definition of Dependency Inversion Principle All three definitions of Dependency Inversion mentioned above mean the same. What each of the definitions imply is that Dependency Inversion Principle fundamentally reverses the way in which dependencies are managed in software systems.

Rather than having the higher-level module directly depending on lower-level modules to carry out their responsibilities, this principle instead makes the higher-level module rely on an 'abstraction' or an 'abstract interface' representing lower-level module. The actual implementation of lower level module can then vary. As long as the lower-level module's implementation is accessible to the higher-level module via the abstract interface, the higher-level module is able to invoke it.
To understand the Dependency Inversion Principle better, let us first take a look at how the traditional procedural systems have their dependencies organised. In procedural systems, higher level modules depend on lower level modules to fulfil their responsibilities. The diagram below shows the procedural dependency structure -
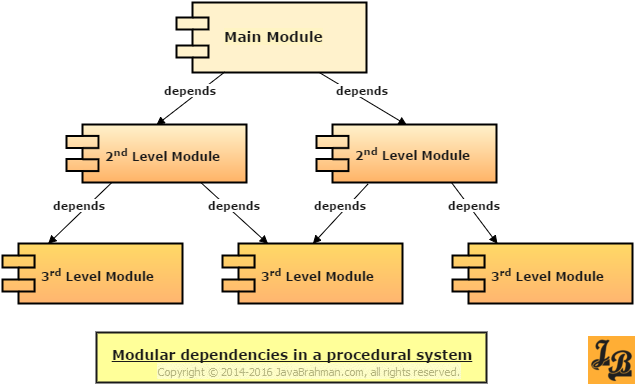As you can see the traditional systems have a top-down dependency structure with the Main or Root module depending on 2^nd Level Modules which in turn depend on 3^rd Level Modules.

The Dependency Inversion Principle, however, advocates that the dependency structure should rather be inverted when designing object-oriented systems.. Have a look at the diagram below showing dependency structure for object-oriented systems - 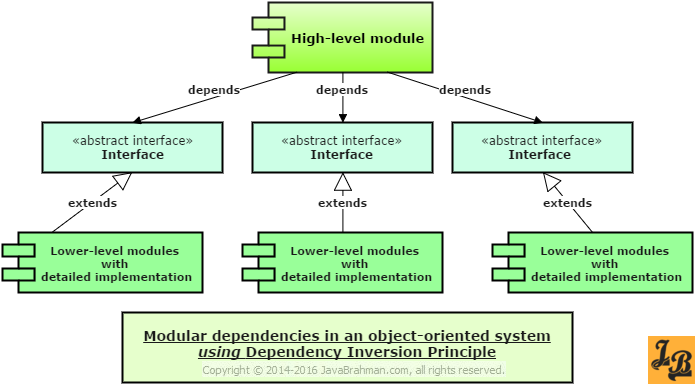In the diagram above, the High-level module does not depend on concrete 2^nd level modules. Instead, the High-level module depends on abstract interfaces which are defined based on the services the High-level module requires from the Lower-level modules.

Secondly, the lower-level modules extend the abstract interfaces. So, when the High-level module invokes the abstract interface, the required task is actually serviced by one of the Lower-level module implementations. Thus, both the High-level module and the Lower-level modules are concerned with the abstract interface structure and depend on it.

Let us now take a look at what are the advantages of using Dependency Inversion Principle when designing object-oriented systems. Advantage of using Dependency Inversion Principle If you take a re-look at the diagram above showing modular dependencies in a procedural system, then one can clearly see the tight coupling that each module layer has with its sub-layer. Thus, any change in the sub-layer will have a ripple effect in the next higher layer and may propagate even further upwards. This tight coupling makes it extremely difficult and costly to maintain and extend the functionality of the layers.

The Dependency Inversion Principle, on the other hand, does away with this tight-coupling between layers by introducing a layer of abstraction between them. So, the higher-level layers, rather than depending directly on the lower-level layers, instead depend on a common abstraction. The lower-level layer can then vary(be modified or extended) without the fear of disturbing higher-level layers depending on it, as long as it obeys the contract of the abstract interface. If, as shown in the object-oriented design diagram above, the lower layers literally extend the abstraction layer interfaces, then they will follow the contract.

Thus, with dependency inversion bringing in the abstraction layer in between the higher and the lower layers, there is a loose coupling between layers which is highly beneficial for maintaining and extending the overall System. Use of Adapter Pattern between abstraction layer and lower-level layer There may arise scenarios where the lower-level layers cannot directly extend the abstraction interfaces. This may happen in cases where the lower-level modules are part of an external library, or the lower-level module is a remote service such as a web-service etc. In such cases an Adapter Design PatternRead tutorial explaining Adapter Pattern implementation is used. Have a look at the diagram below showing how an adapter fits in the design - 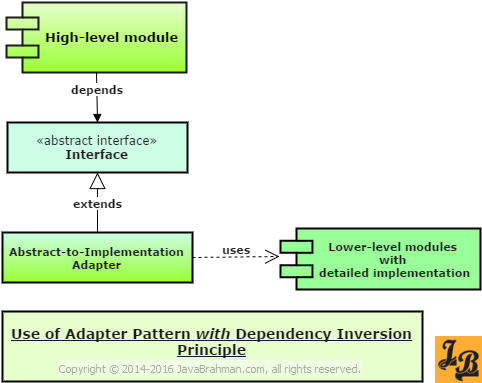As seen in the above diagram, an Adapter can be used to adapt the lower level implementation details to make it comply with the abstraction interface. The higher-level layer, however, remains unaware of the use of adapter pattern as the reference point for the higher layer still remains the abstraction which is left untouched.

Let us now see a much prevalent example of Dependency Inversion Principle - that of the Service layer in the Java Spring framework.
Dependency Inversion Principle - Java Example 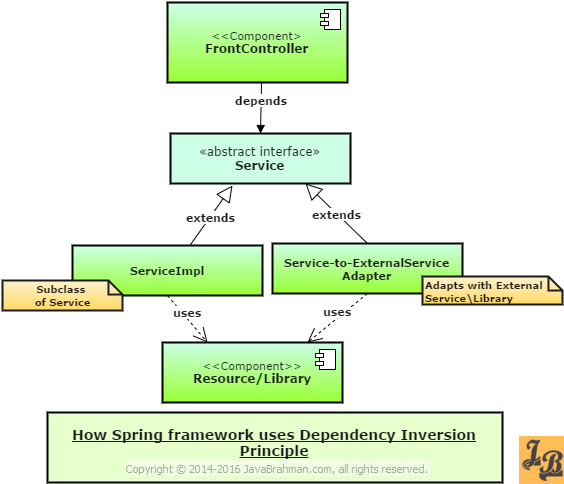The above diagram shows how the Service layer in the Spring framework, a prominent framework of Java Enterprise Edition or JEE, uses Dependency Inversion Principle. The salient observations which can be made from the above diagram are -

• Front Controller component uses the abstraction of a Spring Service.
• The actual Service implementation, ServiceImpl, is provided at run time.
• ServiceImpl extends Service and contains actual implementation logic for talking to Database/Resources.
• In case the Service invokes an external Service/Library, then a Service-to-ExternalService Adapter, which also extends Service abstraction, talks to the external Service/Library.
• The Front Controller layer is loosely coupled with Database/Resource Access layer due to the Service abstraction in between. Hence, changes in lower layers, such as database changes, do not affect the Front Controller unless and until the Service abstraction is unchanged.
• The Service layer in Java Spring Framework thus uses Dependency Inversion Principle for promoting loose coupling and code to abstraction design fundamentals.

Summary In this tutorial we first understood the Dependency Inversion Principle. We then looked at what are the advantages of Dependency Inversion Principle and how Adapter Pattern can also play a crucial part in the implementation of this principle. Lastly, we looked at a Java example showing how the Service layer in the Java Spring Framework uses Dependency Inversion Principle.